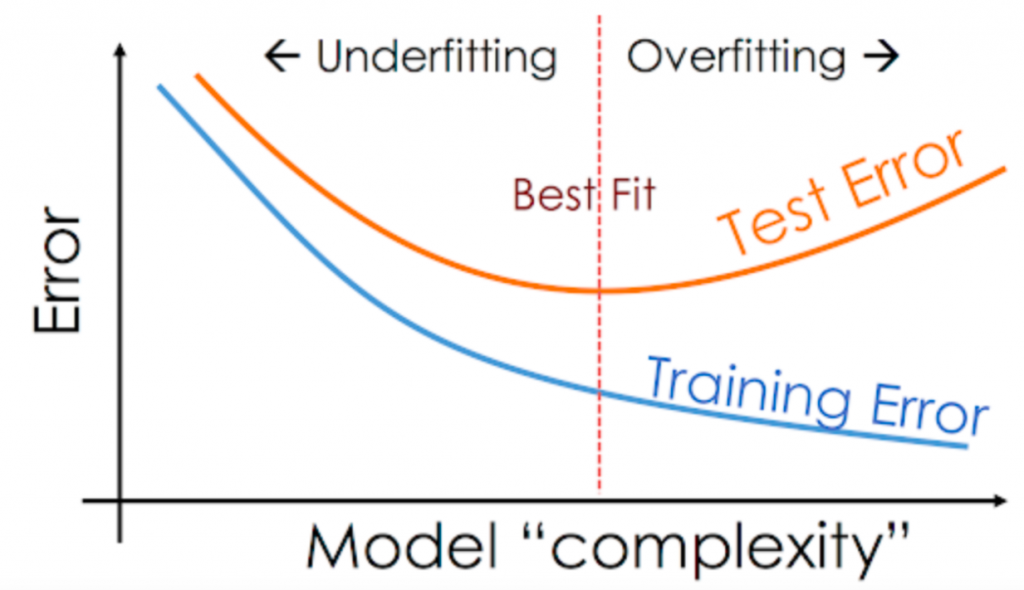
Overfitting using higher order linear regression

The goal of this project is to learn about the concept of overfitting using the Higher order linear regression

Rohan Mandrekar

Last updated on Apr 8, 2021 9 min read blog

https://vitalflux.com/wp-content/uploads/2020/12/overfitting-and-underfitting-wrt-model-error-vs-complexity.png

Switch to dark mode for better readability

What is overfitting?

Overfitting is a concept in data science, which occurs when a statistical model fits exactly against its training data. When this happens, the algorithm unfortunately cannot perform accurately against unseen data, defeating its purpose. Source

How is overfitting different from underfitting?

If overtraining or model complexity results in overfitting, then a logical prevention response would be either to pause training process earlier, also known as, “early stopping” or to reduce complexity in the model by eliminating less relevant inputs. However, if you pause too early or exclude too many important features, you may encounter the opposite problem, and instead, you may underfit your model. Underfitting occurs when the model has not trained for enough time or the input variables are not significant enough to determine a meaningful relationship between the input and output variables. Source

jpg Source

The goal of this project was to learn about the concept of overfitting using higher order linear regression.

Here is the link to the Jupyter Notebook

import numpy as np
import matplotlib.pyplot as plt

Generate 20 data pairs (X, Y) using y = sin(2piX) + 0.1 * N

# rand = np.random.RandomState(20) 
x=np.random.uniform(0,1,20)
print('showing values of x : ',x)

plt.hist(x)
plt.title('values of x')
plt.show()

N=np.random.normal(size=20)
print('showing values of N : ',N)

plt.hist(N)
plt.title('values of N')
plt.show()

showing values of x :  [0.5065955  0.11412767 0.52634393 0.13430513 0.12141921 0.08835001
 0.51724323 0.00444379 0.89216408 0.74439585 0.18419264 0.72286723
 0.59523432 0.95187964 0.27695679 0.43505269 0.95398647 0.33320902
 0.64479291 0.63948439]

png

showing values of N :  [ 1.06510773  0.70313713 -0.45806236 -0.78857958 -0.52984258 -0.84608916
  1.07215212  1.11489313  0.11948624  1.02859731  0.44568169  0.24444456
 -0.86562125 -0.30561877  1.55021314  0.42619426 -0.56210217  0.62200473
  1.00214438  0.03476018]

png

import math
y=[]
for i in range(20):
  # print(i)
  y.append((math.sin(x[i]*3.142*2))+(N[i])*0.2)
print('Values of y : ',y)

plt.hist(y)
plt.title('values of y')
plt.show()

plt.scatter(x,y)
plt.title('all data points')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Values of y :  [0.17118032297090804, 0.7978880906437485, -0.256804412241356, 0.5895734297086033, 0.5851231274205356, 0.3578881765720981, 0.10588092999601144, 0.25089975161344724, -0.6024247587809445, -0.7936818285922409, 1.0049247993821213, -0.936714234036075, -0.736825317156796, -0.35814693610200166, 1.2956949620125484, 0.4817575235401146, -0.3967761741926047, 0.9906810553573294, -0.5892503704887883, -0.7618254109321836]

png

train_y=[]
test_y=[]
train_x=[]
test_x=[]
for i in range(20):
  if(i%2==0):
    train_y.append(y[i])
    train_x.append(x[i])
  else:
    test_y.append(y[i])
    test_x.append(x[i])

print("training set for y : ",train_y)
print("training set for x : ",train_x)
print("test set for y : ",test_y)
print("test set for x : ",test_x)

train_y=np.array(train_y)
test_y=np.array(test_y)
train_x=np.array(train_x)
test_x=np.array(test_x)

train_x=train_x.reshape(-1, 1)
train_y=train_y.reshape(-1, 1)
test_x=test_x.reshape(-1,1)
test_y=test_y.reshape(-1,1)


# plt.scatter(x,train_y)
# plt.title('Training data points')
# plt.xlabel('x')
# plt.ylabel('y')
# plt.show()

# plt.scatter(x,test_set)
# plt.title('Training data points')
# plt.xlabel('x')
# plt.ylabel('y')
# plt.show()

training set for y :  [0.17118032297090804, -0.256804412241356, 0.5851231274205356, 0.10588092999601144, -0.6024247587809445, 1.0049247993821213, -0.736825317156796, 1.2956949620125484, -0.3967761741926047, -0.5892503704887883]
training set for x :  [0.5065954955910669, 0.5263439330297612, 0.1214192124185125, 0.5172432303376305, 0.8921640831936551, 0.18419264043506622, 0.5952343194155714, 0.2769567933749101, 0.9539864651937019, 0.6447929132040842]
test set for y :  [0.7978880906437485, 0.5895734297086033, 0.3578881765720981, 0.25089975161344724, -0.7936818285922409, -0.936714234036075, -0.35814693610200166, 0.4817575235401146, 0.9906810553573294, -0.7618254109321836]
test set for x :  [0.11412767018169767, 0.13430512749327617, 0.08835000898166301, 0.004443786589970133, 0.7443958469077984, 0.7228672268923204, 0.9518796439477641, 0.43505269159444815, 0.33320901738865893, 0.6394843916912883]

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error

Using root mean square error, find weights of polynomial regression for order is 0, 1, 3, 9

# train_x=np.array(train_x)
# train_y=np.array(train_y)
# train_x.reshape(-1)
# train_y.reshape(-1)


# reference : https://moonbooks.org/Articles/How-to-implement-a-polynomial-linear-regression-using-scikit-learn-and-python-3-/
def Regression(i):
    polynomial_features = PolynomialFeatures(degree = i)
    x_transf=polynomial_features.fit_transform(train_x)
    
    model=LinearRegression()
    model.fit(x_transf,train_y)

    y_new=model.predict(x_transf)

    #training error
    rmse=np.sqrt(mean_squared_error(train_y,y_new))
    #test error
    rmse2=np.sqrt(mean_squared_error(test_y,y_new))
    
    r2=r2_score(test_y,y_new)
    
    print('RMSE of degree ',i,': ',rmse2)
    print('R2 of degree ',i,': ',r2)

    return polynomial_features, model

polynomial0, model0 = Regression(0)
weights0=model0.coef_ #https://stackoverflow.com/questions/47303261/getting-weights-of-features-using-scikit-learn-logistic-regression
w0=weights0.copy()
w0.resize(10,refcheck=False) #https://stackoverflow.com/questions/38191855/zero-pad-numpy-array
print('weights for degree 0: ',w0)

polynomial1, model1 = Regression(1)
weights1=model1.coef_  
w1=weights1.copy()
w1.resize(10,refcheck=False)
print('weights for degree 1: ',w1)

polynomial3, model3 = Regression(3)
weights3=model3.coef_
w3=weights3.copy()
w3.resize(10,refcheck=False)
print('weights for degree 3: ',w3)

polynomial9, model9 = Regression(9)
weights9=model9.coef_
w9=weights9.copy()
w9.resize(10,refcheck=False)
print('weights for degree 9: ',w9)

RMSE of degree  0 :  0.6757748998054574
R2 of degree  0 :  -3.095311539746959e-05
weights for degree 0:  [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
RMSE of degree  1 :  0.8812007036292655
R2 of degree  1 :  -0.700430943644264
weights for degree 1:  [ 0.         -2.08588249  0.          0.          0.          0.
  0.          0.          0.          0.        ]
RMSE of degree  3 :  0.8288670295347729
R2 of degree  3 :  -0.5044545024311573
weights for degree 3:  [  0.          19.13481046 -49.59044887  31.84488751   0.
   0.           0.           0.           0.           0.        ]
RMSE of degree  9 :  0.88028613143296
R2 of degree  9 :  -0.6969031211504679
weights for degree 9:  [ 0.00000000e+00 -5.15004633e+05  5.62522625e+06 -3.33866950e+07
  1.19621482e+08 -2.70415048e+08  3.88273313e+08 -3.43304079e+08
  1.70341143e+08 -3.62628790e+07]

Display weights in table

# https://www.geeksforgeeks.org/creating-tables-with-prettytable-library-python/

from prettytable import PrettyTable

mytable=PrettyTable()

columns=['','Order 0','Order 1','Order 3','Order 9']

mytable.add_column(columns[0],['W0','W1','W2','W3','W4','W5','W6','W7','W8','W9'])
mytable.add_column(columns[1],w0)
mytable.add_column(columns[2],w1)
mytable.add_column(columns[3],w3)
mytable.add_column(columns[4],w9)

print(mytable)

+----+---------+--------------------+---------------------+---------------------+
|    | Order 0 |      Order 1       |       Order 3       |       Order 9       |
+----+---------+--------------------+---------------------+---------------------+
| W0 |   0.0   |        0.0         |         0.0         |         0.0         |
| W1 |   0.0   | -2.085882487390529 |  19.134810457045457 | -515004.63279339066 |
| W2 |   0.0   |        0.0         | -49.590448870417305 |  5625226.251401764  |
| W3 |   0.0   |        0.0         |  31.844887505116315 | -33386695.008260697 |
| W4 |   0.0   |        0.0         |         0.0         |  119621482.41552813 |
| W5 |   0.0   |        0.0         |         0.0         |  -270415047.5128739 |
| W6 |   0.0   |        0.0         |         0.0         |  388273313.46595275 |
| W7 |   0.0   |        0.0         |         0.0         |  -343304079.1551127 |
| W8 |   0.0   |        0.0         |         0.0         |  170341143.46188554 |
| W9 |   0.0   |        0.0         |         0.0         |  -36262879.02721146 |
+----+---------+--------------------+---------------------+---------------------+

Draw a chart of fit data

xnew=np.linspace(0,1,100)
xnew=np.array(xnew)
xnew=xnew.reshape(-1,1)

x_trans0=polynomial0.fit_transform(xnew)
y0=model0.predict(x_trans0)
plt.scatter(x,y)
plt.plot(xnew,y0,c='r')
plt.title('polynomial regression order 0')
plt.xlabel('x')
plt.ylabel('y')
plt.show()


x_trans1=polynomial1.fit_transform(xnew)
y1=model1.predict(x_trans1)
plt.scatter(x,y)
plt.plot(xnew,y1,c='r')
plt.title('polynomial regression order 1')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

x_trans3=polynomial3.fit_transform(xnew)
y3=model3.predict(x_trans3)
plt.scatter(x,y)
plt.plot(xnew,y3,c='r')
plt.title('polynomial regression order 3')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

x_trans9=polynomial9.fit_transform(xnew)
y9=model9.predict(x_trans9)
plt.scatter(x,y)
plt.plot(xnew,y9,c='r')
plt.title('polynomial regression order 9')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

png

Draw train error vs test error

train_errors=[]
test_errors=[]
# print(test_x.shape)
# print(test_y.shape)

for i in range (0,10):
  polynomial_features = PolynomialFeatures(degree = i)
  x_transf=polynomial_features.fit_transform(train_x)
    
  model=LinearRegression()
  model.fit(x_transf,train_y)

  y_new=model.predict(x_transf)

  #training error
  rmse=np.sqrt(mean_squared_error(train_y,y_new))
  #test error
  x_transf=polynomial_features.fit_transform(test_x)
  y_new=model.predict(x_transf)
  rmse2=np.sqrt(mean_squared_error(test_y,y_new))

  train_errors.append(rmse)
  test_errors.append(rmse2)


print(train_errors)
print(test_errors)
models= np.linspace(0, 9, 10)
plt.plot(models,train_errors,label = 'train error', color = 'blue')
plt.plot(models,test_errors,label = 'test error', color = 'red')
plt.title('Train vs test error')
plt.xlabel('polynomial regression order')
plt.ylabel('RMSE')
plt.legend()
plt.show()

[0.6718839839061639, 0.3949820650144116, 0.362185294183138, 0.15509957090719734, 0.1257616863153283, 0.11667502425249053, 0.11033312782105564, 0.05139960801508042, 0.045984709291081345, 2.7116532461094445e-08]
[0.6757748998054574, 0.5130767396803901, 0.6430332529224712, 0.40209758302055293, 0.7368997594930184, 0.3663105838641724, 0.5101256658169809, 6.711239341941148, 37.9374792351037, 5445.918996816799]

png

generate 100 more data and fit 9th order model and draw fit

# x2=np.random.uniform(0,1,100)
x2=np.linspace(0,1,100)
n2=np.random.normal(size=100)

print('showing values of x : ',x2)

plt.hist(x2)
plt.title('values of x2')
plt.show()

print('showing values of n2 : ',n2)

plt.hist(n2)
plt.title('values of n2')
plt.show()

showing values of x :  [0.         0.01010101 0.02020202 0.03030303 0.04040404 0.05050505
 0.06060606 0.07070707 0.08080808 0.09090909 0.1010101  0.11111111
 0.12121212 0.13131313 0.14141414 0.15151515 0.16161616 0.17171717
 0.18181818 0.19191919 0.2020202  0.21212121 0.22222222 0.23232323
 0.24242424 0.25252525 0.26262626 0.27272727 0.28282828 0.29292929
 0.3030303  0.31313131 0.32323232 0.33333333 0.34343434 0.35353535
 0.36363636 0.37373737 0.38383838 0.39393939 0.4040404  0.41414141
 0.42424242 0.43434343 0.44444444 0.45454545 0.46464646 0.47474747
 0.48484848 0.49494949 0.50505051 0.51515152 0.52525253 0.53535354
 0.54545455 0.55555556 0.56565657 0.57575758 0.58585859 0.5959596
 0.60606061 0.61616162 0.62626263 0.63636364 0.64646465 0.65656566
 0.66666667 0.67676768 0.68686869 0.6969697  0.70707071 0.71717172
 0.72727273 0.73737374 0.74747475 0.75757576 0.76767677 0.77777778
 0.78787879 0.7979798  0.80808081 0.81818182 0.82828283 0.83838384
 0.84848485 0.85858586 0.86868687 0.87878788 0.88888889 0.8989899
 0.90909091 0.91919192 0.92929293 0.93939394 0.94949495 0.95959596
 0.96969697 0.97979798 0.98989899 1.        ]

png

showing values of n2 :  [-1.55866377e+00 -1.36082128e+00 -1.05110994e+00  1.04086891e+00
  2.96452186e-01 -1.05815554e+00  1.02215584e+00  7.60582413e-01
  1.95520316e-01  9.15855074e-01  1.19469760e+00  1.08410113e+00
  1.03857214e-01  5.98172298e-01 -4.46541456e-01 -2.80242879e-01
 -2.67079929e+00 -2.78362843e+00 -2.52092922e-01  5.87267337e-01
  3.51216092e-01  1.26619371e+00  6.17943671e-01 -1.44713393e+00
 -1.25583113e+00  1.42049206e+00 -1.11409691e+00 -4.55209331e-01
 -3.44930931e-01 -1.46415939e+00 -1.04930766e+00 -1.52506917e+00
  1.02117993e+00  6.25609487e-02 -8.40164086e-01  5.24914195e-01
  6.09723066e-01  8.19633625e-01 -7.27630828e-01  4.75948243e-01
 -1.64089928e+00  4.39467458e-01  4.21874275e-01 -1.34377280e-01
  1.33547374e+00  5.53856620e-02 -2.54380300e-04  9.48876627e-01
  8.90043657e-01 -1.78931297e-01 -9.16446072e-01  9.90562129e-01
  8.88212853e-01  1.69680671e-01  8.14319143e-01  6.12007163e-01
  1.39683318e-01  8.71915540e-01 -7.63908904e-01 -1.17811912e+00
 -9.17932742e-01 -6.39680044e-01 -1.90497738e-01 -9.99193965e-01
  3.64166255e-01 -3.91968107e-01 -7.05899449e-01 -4.43756310e-01
  6.40494524e-01 -1.40481471e+00 -3.35706079e+00 -5.48380794e-01
 -2.11144296e-01 -1.10600220e+00 -7.95820110e-01 -6.79240687e-01
 -1.52953134e+00 -1.60538107e-01  3.29946743e-01 -8.81889112e-01
  1.35867475e+00 -4.08459188e-03 -2.02817090e+00  6.65982192e-01
 -1.67109931e+00 -6.05020469e-01 -7.24295867e-01  5.95801125e-01
 -4.20600058e-01 -8.75747834e-01  1.25075185e-02  1.26851542e+00
 -1.08861724e+00 -3.87161159e-01  9.77170225e-01  7.82021728e-01
 -4.89046218e-01 -2.81539170e-01  3.93538608e-01 -2.13785821e-01]

png

y2=[]
for i in range(100):
  # print(i)
  y2.append((math.sin(x2[i]*3.142*2))+(n2[i])*0.2)
print('Values of y2 : ',y2)

plt.hist(y2)
plt.title('values of y2')
plt.show()

plt.scatter(x2,y2)
plt.title('scatter plot of 100 data points')
plt.show()

x2=np.array(x2)
y2=np.array(y2)
x2=x2.reshape(-1,1)
y2=y2.reshape(-1,1)

Values of y2 :  [-0.3117327532333845, -0.2087321237010215, -0.08361320756022472, 0.3974492687128643, 0.3104702861353639, 0.10044142819925178, 0.5761394617072048, 0.581963406665068, 0.5253583271126174, 0.7238741365917095, 0.8319137142946355, 0.8596771765088341, 0.7109219200919744, 0.8542987508380389, 0.6869108133829285, 0.7585989713174226, 0.3156349828291035, 0.32479373814101953, 0.8592749347810785, 1.0516571172768014, 1.0251943153815195, 1.225091038921837, 1.1084279088007505, 0.7044326395540844, 0.7477104914536655, 1.283969255314285, 0.7740184140652548, 0.8987479304584214, 0.909769042934862, 0.6709466594277712, 0.7350585124815525, 0.6172418704097319, 1.1001127901453875, 0.8784017794561514, 0.6643820215540022, 0.9005702172282631, 0.8775001506965499, 0.8764072775392451, 0.5210097503891915, 0.713096327364823, 0.23860884836693852, 0.6012813720422497, 0.5422941436365291, 0.37373088330499327, 0.608774620541279, 0.29245435537410486, 0.21989039772205776, 0.34739479455999395, 0.2726715533827463, -0.0044613573266350515, -0.2154283991453561, 0.10263860107351973, 0.01921864488010891, -0.1867998099519069, -0.11929507784064178, -0.22004398728221192, -0.37341600521489854, -0.2842602853864343, -0.666868624877389, -0.8030835349977477, -0.8021335754328731, -0.7950790350602879, -0.7511515268655266, -0.9559277723581943, -0.7232474356255517, -0.9112596483739628, -1.0074767301682954, -0.9849897395880294, -0.7944714385077226, -1.2261493220746884, -1.6354076579703123, -1.0885981012869317, -1.0321344493944529, -1.218102643406947, -1.1590476261102738, -1.1346859192184795, -1.2996752179980313, -1.0168051446232313, -0.9056706908267995, -1.1310868317006366, -0.6621777570024268, -0.9101718097941586, -1.286768655718661, -0.7161686849729711, -1.1483946530370577, -0.8967093068368315, -0.8789705081713302, -0.5704004580374775, -0.7263527052172503, -0.7674675565155138, -0.5375161080715276, -0.23183912558195263, -0.6468346412811318, -0.44838408248155437, -0.11586438306168112, -0.09398684596579335, -0.28628470022161423, -0.18210843498848756, 0.01608866247606501, -0.041942471431624724]

png

polynomial_features2=PolynomialFeatures(degree=9)
x_transf2=polynomial_features2.fit_transform(x2)
model2=LinearRegression()
model2.fit(x_transf2,y2)

y2new=model2.predict(x_transf2)

xnew=np.linspace(0,1,100)
plt.plot(xnew,y2new,c='r')
plt.scatter(x2,y2)
plt.title('plot for 100 data points, degree 9 polynomial regression')
plt.xlabel('x')
plt.ylabel('y')
plt.show

<function matplotlib.pyplot.show>

png

Now we will regularize using the sum of weights

from sklearn.linear_model import Ridge
#https://inria.github.io/scikit-learn-mooc/python_scripts/linear_models_regularization.html
def l2ridge(x2,y2,alpha):
  # x2=x2.reshape(100,1)
  # y2=y2.reshape(100,1)  
  # polynomial_features3=PolynomialFeatures(degree=9)
  ridge = make_pipeline(PolynomialFeatures(degree=9),
                      Ridge(alpha=alpha))
  # transform=polynomial_features3.fit_transform(x2)
  # ridge=Ridge(alpha=alpha)
  ridge.fit(x2,y2)
  result=ridge.predict(x2)
  return result

Draw chart for lambda is 1, 1/10, 1/100, 1/1000, 1/10000, 1/100000

y2new1=l2ridge(x2,y2,1)
plt.scatter(x2,y2)
plt.plot(xnew,y2new1,c='r')
plt.title('lambda=1')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

y2new10=l2ridge(x2,y2,1/10)
plt.scatter(x2,y2)
plt.plot(xnew,y2new10,c='r')
plt.title('lambda=1/10')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

y2new100=l2ridge(x2,y2,1/100)
plt.scatter(x2,y2)
plt.plot(xnew,y2new100,c='r')
plt.title('lambda=1/100')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

y2new1000=l2ridge(x2,y2,1/1000)
plt.scatter(x2,y2)
plt.plot(xnew,y2new1000,c='r')
plt.title('lambda=1/1000')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

y2new10000=l2ridge(x2,y2,1/10000)
plt.scatter(x2,y2)
plt.plot(xnew,y2new10000,c='r')
plt.title('lambda=1/10000')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

y2new100000=l2ridge(x2,y2,1/100000)
plt.scatter(x2,y2)
plt.plot(xnew,y2new100000,c='r')
plt.title('lambda=1/100000')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

y2new1000000000=l2ridge(x2,y2,1/1000000000)
plt.scatter(x2,y2)
plt.plot(xnew,y2new1000000000,c='r')
plt.title('lambda=1/1000000000')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

png

Now draw test and train error according to lamda

regularised_train_error=[]
regularised_test_error=[]
alphas=[1,1/10,1/100,1/1000,1/10000,1/100000,1/1000000,1/10000000,1/100000000,1/1000000000]
for alpha in alphas:
  
  # polynomial_features = PolynomialFeatures(degree = i)
  # x_transf=polynomial_features.fit_transform(train_x)
    
  # model=LinearRegression()
  # model.fit(x_transf,train_y)

  # y_new=model.predict(x_transf)
  ridge = make_pipeline(PolynomialFeatures(degree=9),
                      Ridge(alpha=alpha))
  ridge.fit(train_x,train_y)
  ynew=ridge.predict(train_x)

  #training error
  rmse=np.sqrt(mean_squared_error(train_y,ynew))
  #test error
  y2newtest=ridge.predict(test_x)
  rmse2=np.sqrt(mean_squared_error(test_y,y2newtest))

  regularised_train_error.append(rmse)
  regularised_test_error.append(rmse2)


print(train_errors)
print(test_errors)
logalpha=[np.log(1),np.log(1/10),np.log(1/100),np.log(1/1000),np.log(1/10000),np.log(1/100000),np.log(1/1000000),np.log(1/10000000),np.log(1/100000000),np.log(1/1000000000)]
plt.plot(logalpha,regularised_train_error,label = 'train error', color = 'blue')
plt.plot(logalpha,regularised_test_error,label = 'test error', color = 'red')
plt.title('train vs test error for regularized ')
plt.xlabel('ln(lambda)')
plt.ylabel('error')
plt.legend()
plt.show()

[0.6718839839061639, 0.3949820650144116, 0.362185294183138, 0.15509957090719734, 0.1257616863153283, 0.11667502425249053, 0.11033312782105564, 0.05139960801508042, 0.045984709291081345, 2.7116532461094445e-08]
[0.6757748998054574, 0.5130767396803901, 0.6430332529224712, 0.40209758302055293, 0.7368997594930184, 0.3663105838641724, 0.5101256658169809, 6.711239341941148, 37.9374792351037, 5445.918996816799]

png

Based on best performance my model will be the one with lambda 1/1000000 because here the difference between train and test error is almost negligible, it has lowest test error compared to other models, and the error is lesser than the error of the model with lambda 1/1000000000.

Challenges faced:

Initially I struggled with implimenting polynomial regression, but this blog helped me understand the concept and how to implement it.

While adding the weights of the polynomials to the pretty table, i had to pad zeroes to it, to make all of them of the same length. But doing so messed up the weights of all the polynomials because it was a referenced variable. Using the .copy() function solved that problem for me.

I also struggled while trying to plot the graph for ‘Train vs test error’ for polynomial regression of each order. My TA helped me out by pointing out where I went wrong.